Desmos Project
Here is a LINK to my graph.
I wasn't sure what I wanted to draw at first so I looked up soccer drawings on desmos. A FC Barcelona logo came up so I though it would be cool to make. I had to do a lot of trial and error but in the end I think it worked out great. I had to look up some of the equations I used for example the hyperbolas and the ellipses. I was struggling to figure out how to use them some I use the ones from a drawing I found so I wouldn't spend hours and hours on just that part.
Doing this drawing did help me understand the equations more. I was able to actually use them so I could understand how to use them better. I understand linear equations better because I used a lot of them in my picture. I already knew how to use them but I was using them a lot. (y=mx+b) b is where is line intercepts the y-axis, m is the slope of the line. Another equation I learned more about is circles.
((x-h)squared + (y-k)squared = r squared) h and k change the location of the circle and r changes the radius.
Doing this drawing did help me understand the equations more. I was able to actually use them so I could understand how to use them better. I understand linear equations better because I used a lot of them in my picture. I already knew how to use them but I was using them a lot. (y=mx+b) b is where is line intercepts the y-axis, m is the slope of the line. Another equation I learned more about is circles.
((x-h)squared + (y-k)squared = r squared) h and k change the location of the circle and r changes the radius.
Unit 3 Reflection
Q1: What content/skills have been most interesting to you?
Q2: How have you grown mathematically?
1.) I find volume interesting because I will use that in many different situations like finding how much dirt I will need to build bike trails and jumps.
2.) I have grown by learning about volume and surface area. I did not know how to find volume or surface area before now.
Q2: How have you grown mathematically?
1.) I find volume interesting because I will use that in many different situations like finding how much dirt I will need to build bike trails and jumps.
2.) I have grown by learning about volume and surface area. I did not know how to find volume or surface area before now.
POWs
The POWs have helped me think in different ways. There have been various different POWs so I have gotten to think in many different ways. They have helped me with my problem solving the most because all of the problems required that skill. The POWs have helped me master the mathematical skills I have learned.
Ideal Size Of A Soda Can
Problem Statement
What is the ideal size of a 12-ounce soda can? From the perspective of the company, “ideal” means the soda can that will cost the least. We need to find the smallest amount of aluminum, smallest surface area, for the given volume. Find the radius and the height of a cylindrical can that holds 355cm cubed and uses the smallest amount of aluminum.
Process And Solution
I started by choosing radius’ 1-8 and solving what the height for each radius is. I made a table to keep organized. To do that, I used the equation below.
πr squared times height = 355cm squared
Then I made another table that had radius, height, and surface area. I inserted the radius and the height into the table then used another equation to solve for surface area (below).
2πr times height + 2πr squared = surface area
After I found the surface area of every radius I decided that a soda can with a radius of 4, and a height of 7.06 had the least amount of surface area. The surface area is 277.97cm squared.
Questioning The Result
My answer does not correspond to the current size of a soda can. I think that factories are not making the soda cans with the least amount of surface area because they want to have the most drink also. And you would have less drink if you used the least surface area soda can compared to the soda can they are using.
Evaluation
This pow made me think about volume and area, which I usually don’t think about. I also had to use a few different crazy equations, which messed with my brain a bit. I asked my peers for help when I got stuck and I also talked to them about what they had found to.
What is the ideal size of a 12-ounce soda can? From the perspective of the company, “ideal” means the soda can that will cost the least. We need to find the smallest amount of aluminum, smallest surface area, for the given volume. Find the radius and the height of a cylindrical can that holds 355cm cubed and uses the smallest amount of aluminum.
Process And Solution
I started by choosing radius’ 1-8 and solving what the height for each radius is. I made a table to keep organized. To do that, I used the equation below.
πr squared times height = 355cm squared
Then I made another table that had radius, height, and surface area. I inserted the radius and the height into the table then used another equation to solve for surface area (below).
2πr times height + 2πr squared = surface area
After I found the surface area of every radius I decided that a soda can with a radius of 4, and a height of 7.06 had the least amount of surface area. The surface area is 277.97cm squared.
Questioning The Result
My answer does not correspond to the current size of a soda can. I think that factories are not making the soda cans with the least amount of surface area because they want to have the most drink also. And you would have less drink if you used the least surface area soda can compared to the soda can they are using.
Evaluation
This pow made me think about volume and area, which I usually don’t think about. I also had to use a few different crazy equations, which messed with my brain a bit. I asked my peers for help when I got stuck and I also talked to them about what they had found to.
Circular Pie
Problem Statement:
You are given a circular pie and you can only use cuts that go all the way through the pie. Your cuts do not have to go through the center of the pie, but they have to be straight cuts. Your goal is to find the highest amount of pieces you can get with the least amount of cuts. Going up to 5 or 6 cuts is okay. The pieces do not have to be the same size.
Process:
I approached the problem with trial and error. I was not exactly sure how I would figure out what the highest amount of pieces would be so I just started making circles and seeing if I could get the most pieces. After a while passed with this process someone suggested that I put my data into a table. After I put my data into a table I discovered a pattern. In the Y column, the number seemed to be increasing by a certain number each time, but I wasn’t exactly sure by how much yet.. For example when X=0 and Y=1, then X=1 and Y=2, then X=2 and Y=4, then X=3 and Y=7.
Solution:
I soon realized the equation. f(x) = x + f(x - 1) I tried this equation and it worked. I used this equation on many numbers so that I could make sure that it worked. I found the number of cuts needed for the greatest amount of pieces for all the numbers up to 9 while using this equation.
Extension:
Adding on to the problem, find the least amount of pieces you can get with each number of cuts on your table. Find an equation for this as well if possible.
Evaluation:
I though this was a good problem solving problem. It was difficult because for some reason I was not trying to find a pattern in a table, I was trying to find the slices in the pies. I had to think of it in a different way, not using a ruler and a pencil. I enjoyed this problem. It was difficult, interesting, and now I know how to cut my pie when lots of friends come over. I would give myself a 22/25. I thought I did a good job on this.
You are given a circular pie and you can only use cuts that go all the way through the pie. Your cuts do not have to go through the center of the pie, but they have to be straight cuts. Your goal is to find the highest amount of pieces you can get with the least amount of cuts. Going up to 5 or 6 cuts is okay. The pieces do not have to be the same size.
Process:
I approached the problem with trial and error. I was not exactly sure how I would figure out what the highest amount of pieces would be so I just started making circles and seeing if I could get the most pieces. After a while passed with this process someone suggested that I put my data into a table. After I put my data into a table I discovered a pattern. In the Y column, the number seemed to be increasing by a certain number each time, but I wasn’t exactly sure by how much yet.. For example when X=0 and Y=1, then X=1 and Y=2, then X=2 and Y=4, then X=3 and Y=7.
Solution:
I soon realized the equation. f(x) = x + f(x - 1) I tried this equation and it worked. I used this equation on many numbers so that I could make sure that it worked. I found the number of cuts needed for the greatest amount of pieces for all the numbers up to 9 while using this equation.
Extension:
Adding on to the problem, find the least amount of pieces you can get with each number of cuts on your table. Find an equation for this as well if possible.
Evaluation:
I though this was a good problem solving problem. It was difficult because for some reason I was not trying to find a pattern in a table, I was trying to find the slices in the pies. I had to think of it in a different way, not using a ruler and a pencil. I enjoyed this problem. It was difficult, interesting, and now I know how to cut my pie when lots of friends come over. I would give myself a 22/25. I thought I did a good job on this.
Unit 2 Reflection
What has been the work you are most proud of in this unit?
The work I am most proud of in this unit is the word problems that involve trig. At first I did not fully understand trig but through all of the word problems that we have done, I have gotten much better at it.
Q2: What skills are you developing in geometry/math?
I am mostly learning about trigonometry. Trig is the solving of triangle's sides and even angles.
Q3: Choose one topic: similarity (ratios) or trigonometry. Explain what it is. Provide an example of how it is used in mathematics to solve problems. State an application of the topic in the adult world that interests you (i.e. scaled replicas of sculptures, gearing ratios, scaled models for architecture, trigonometry in construction or blood splatter analysis, etc).
The work I am most proud of in this unit is the word problems that involve trig. At first I did not fully understand trig but through all of the word problems that we have done, I have gotten much better at it.
Q2: What skills are you developing in geometry/math?
I am mostly learning about trigonometry. Trig is the solving of triangle's sides and even angles.
Q3: Choose one topic: similarity (ratios) or trigonometry. Explain what it is. Provide an example of how it is used in mathematics to solve problems. State an application of the topic in the adult world that interests you (i.e. scaled replicas of sculptures, gearing ratios, scaled models for architecture, trigonometry in construction or blood splatter analysis, etc).
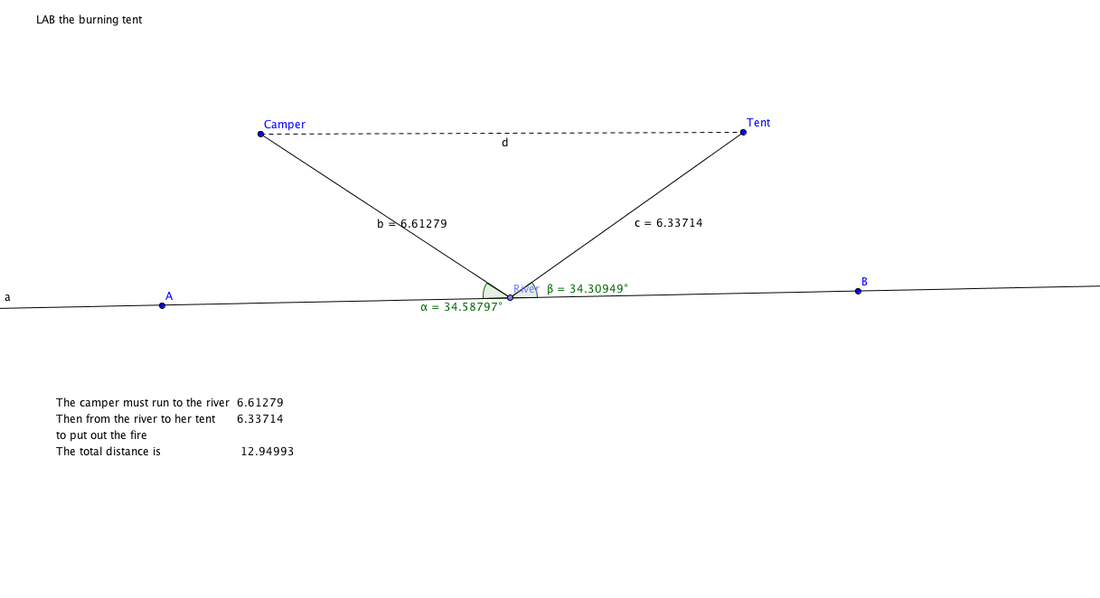
The Burning Tent Problem
Both of the angles seem to be almost the same.
The path camper to tent is the shortest because the distance for a straight path will be shorter than a path that has to go down then up.
The point river needs to be right in the middle of line camper/tent in order for it to be at its smallest length.
The path camper to tent is the shortest because the distance for a straight path will be shorter than a path that has to go down then up.
The point river needs to be right in the middle of line camper/tent in order for it to be at its smallest length.
Tessellation Project
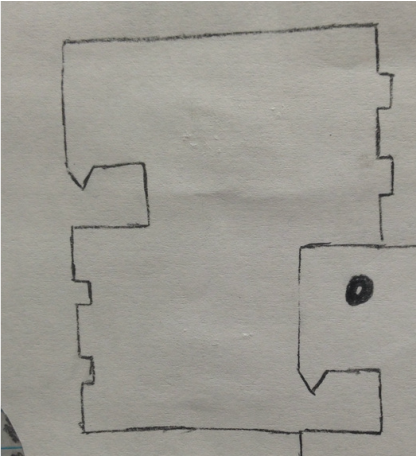
The Theme of my tessellation is a dinosaur. I chose a dinosaur tessellation because I like dinosaurs. When I made made my dinosaur i started with a rectangle. I googled some dinosaur tessellations so I could get an idea of how to make it. I found the tessellation that is mine on the internet and thought that it would be a fun one to do. So I sorta copied that one off the internet and modified it a little bit. I added where the little arms are. I added this so I wasn't just copying it off the internet. I think that tessellations are more art because they feel more like art rather than math. I think that if I saw a tessellation and didn't know much about them I would think "oh that is some cool art," not "oh that is some cool math." I believe that tessellations are more art rather than math because thay remind me more of art then math.
I started my tessellation with a rectangle. I then made two little indents into the bottom left side of the rectangle. I moved the pieces that I pulled out and put them on the top right of the rectangle. I then saw a dinosaur forming, I then made a mouth in the top right of the rectangle. after I made a mouth, I had to make sure that the dinosaurs would line up so I had to make a place for its face in the bottom left on the rectangle. I made it look like a tail.
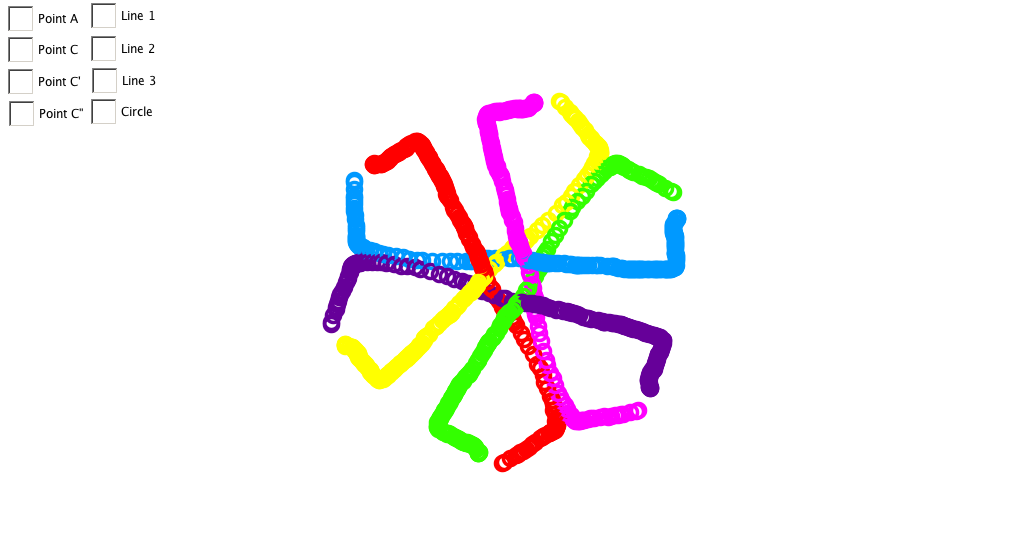
Sail Trail Graffiti
Reflection
I constructed the Sails by using Geogabra. I made a circle, made some points, made some lines through the circle using the points, then I reflected a few points over some lines. My creation creates perfect symmetry because no matter where you move your one point all the others will move in the same way making it symmetric. I think that this makes really good rotational symmetry because you can rotate it and it will map on top of itself 3 times within 360 degrees.